

















Do you want to contribute by writing guest posts on this blog?
Please contact us and send us a resume of previous articles that you have written.
Unveiling the Secrets of Trigonometry: Exploring Trigonometric Functions and Equations!

Trigonometry is a fundamental branch of mathematics that deals with the relationships between the angles and sides of triangles. It is a powerful tool that allows us to understand and solve various real-world problems involving angles, distances, and heights. In this article, we will dive into the world of trigonometry and explore the fascinating concepts of trigonometric functions and equations.
Understanding Trigonometric Functions
In trigonometry, functions are the building blocks that help us analyze and solve problems related to angles. Trigonometric functions relate the ratios of the sides of a right triangle to its angles.
1. Sine Function (sin)
The sine function (sin) is one of the most fundamental trigonometric functions. It relates the ratio of the length of the side opposite an angle to the hypotenuse (the longest side) of a right triangle.
4 out of 5
| Language | : | English |
| File size | : | 11882 KB |
| Text-to-Speech | : | Enabled |
| Screen Reader | : | Supported |
| Enhanced typesetting | : | Enabled |
| Print length | : | 182 pages |
| Lending | : | Enabled |
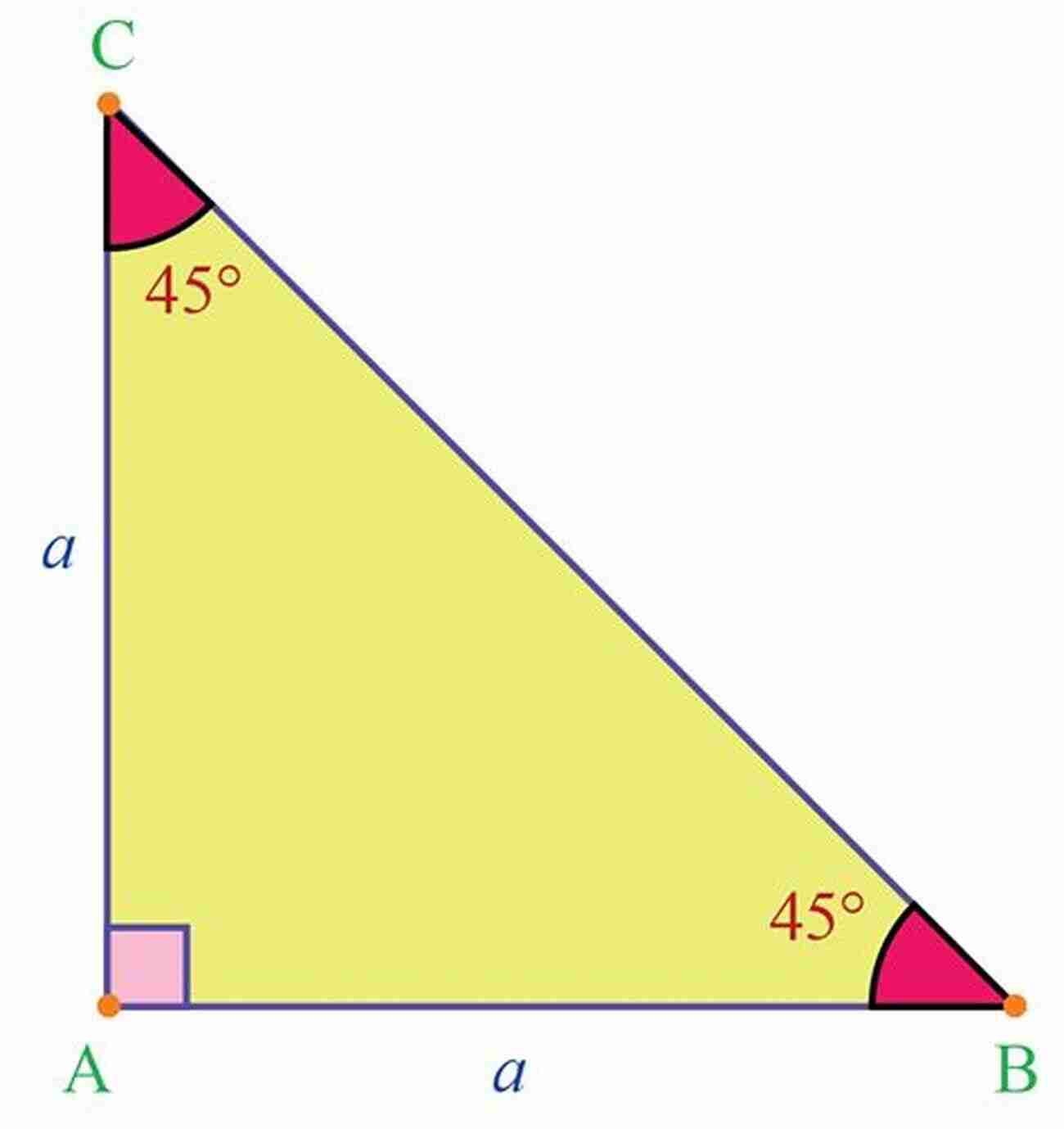
To calculate the sine of an angle, you divide the length of the side opposite the angle by the length of the hypotenuse. This ratio can be represented as sin(angle) = opposite/hypotenuse. The resulting value lies between -1 and 1.
The sine function is widely used in various fields such as engineering, physics, and architecture. It helps in measuring distance, analyzing periodic phenomena, and constructing accurate structures.
2. Cosine Function (cos)
The cosine function (cos) is another important trigonometric function. It relates the ratio of the length of the side adjacent to an angle to the hypotenuse of a right triangle.
To calculate the cosine of an angle, you divide the length of the side adjacent to the angle by the length of the hypotenuse. This ratio can be represented as cos(angle) = adjacent/hypotenuse. Like the sine function, the resulting value lies between -1 and 1.
The cosine function is widely used in fields such as navigation, motion analysis, and signal processing. It helps in determining direction, studying circular movements, and filtering out unwanted noise from signals.
3. Tangent Function (tan)
The tangent function (tan) is derived from the sine and cosine functions. It represents the ratio of the length of the side opposite an angle to the length of the side adjacent to the angle.
To calculate the tangent of an angle, you divide the length of the side opposite the angle by the length of the side adjacent to the angle. This ratio can be represented as tan(angle) = opposite/adjacent.
The tangent function is particularly useful in fields such as engineering, astronomy, and computer graphics. It helps in calculating slopes, predicting celestial events, and rendering realistic 3D scenes.
Solving Trigonometric Equations
Trigonometric equations involve trigonometric functions and angles. Solving these equations helps us find unknown angles, sides, or ratios in a given triangle.
1. Pythagorean Identity
The Pythagorean identity is a fundamental equation in trigonometry. It relates the three main trigonometric functions (sin, cos, and tan) using the Pythagorean theorem.
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Using this theorem, we can derive the Pythagorean identity:
sin^2(angle) + cos^2(angle) = 1
This identity allows us to use the values of sine and cosine to find the value of the other trigonometric functions.
2. Solving Trigonometric Equations
The process of solving trigonometric equations involves manipulating trigonometric functions and using trigonometric identities to simplify the equation. By using algebraic techniques and applying trigonometric properties, we can find the values of angles or ratios that satisfy the equation.
Trigonometric equations find applications in various fields such as physics, engineering, and architecture. They help in determining angles of inclination, calculating forces, and designing stable structures.
Trigonometry, with its trigonometric functions and equations, unlocks the mysteries of angles and triangles. Through the sine, cosine, and tangent functions, we can understand and analyze the relationships between the sides and angles of a right triangle. By solving trigonometric equations, we can find missing angles and ratios, enabling us to solve real-world problems in different fields.
Whether in architecture, physics, astronomy, or any other discipline, the applications of trigonometry are far-reaching. So, let's embrace the power of trigonometry and unlock a whole new dimension of understanding in our world!
4 out of 5
| Language | : | English |
| File size | : | 11882 KB |
| Text-to-Speech | : | Enabled |
| Screen Reader | : | Supported |
| Enhanced typesetting | : | Enabled |
| Print length | : | 182 pages |
| Lending | : | Enabled |
trigonometry, trigonometric functions, calculation of values of trigonometric functions, trigonometric reduction formulas, reference angles, calculation of values of trigonometric functions of arbitrary angle x examples, relationships between trigonometric functions of the same angle, relationships between trigonometric functions of the same angle shown in unit circle, relationships between trigonometric functions of the same angle shown in the tabular form, relationships between trigonometric functions of the same angle examples, addition formulas and related identities, sum and difference formulas for trigonometric functions, deriving addition formulas for sine and cosine functions, addition formulas for tangent and cotangent functions, trigonometric functions of double angles, double angle formulas, trigonometric functions expressed by half angle, trigonometric functions of double angles expressed by tangent function, trigonometric functions expressed by tangent of half angle, half angle formulas, trigonometric functions expressed by cosine of double angle, sum to product and product to sum formulas or identities, sum to product formulas for sine and cosine functions, sum to product formulas for tangent and cotangent functions, product to sum formulas for sine and cosine functions, trigonometric identities examples, graphs of trigonometric functions, graph of sine function f(x) = sin x, properties of sine function, domain and range of sine function, roots or zeros of sine function, extremes maximum and minimum of sine function, parity and periodicity of sine function, behaviour of sine function, graph of cosine function f(x) = cos x, properties of cosine function, domain and range zeros of cosine function, roots or zeros of cosine function, extremes maximum and minimum of cosine function, parity and periodicity of cosine function, behaviour of cosine function, graph of tangent function f(x) = tan x, properties of tangent function, domain and range of tangent function, roots or zeros of tangent function, parity and periodicity of tangent function, tangent function behavior and monotony, graph of cotangent function f(x) = cot x, properties of cotangent function, domain and range of cotangent function, roots or zeros of cotangent function, parity and periodicity of cotangent function, cotangent function behavior and monotony, graph of function y = asin (bx + c),graph of function y = asin x, graph of function y = sin bx, graph of function y = sin (x + c),graph of function y = asin (bx + c),graph of function y = acos (bx + c),graphs of functions y = asin (bx + c) and y = acos (bx + c) examples, trigonometric functions and inverse trigonometric functions, trigonometric functions graphs and relations, sine function and cosine function graphs and relations, tangent function and cotangent function graphs and relations, cosecant function and secant function graphs and relations, cosecant function y = csc x, graph of cosecant function, secant function y = sec x, graph of secant function, inverse trigonometric functions or arc-functions and their graphs, inverse trigonometric functions arc-functions, arc-sine function and arc-cosine function, arc-sine function y = arcsin x, arc-cosine function y = arccos x, graph of arc-sine function and arc-cosine function, arc-tangent function and arc-cotangent function, arc-tangent function y = arctan x, arc-cotangent function y = arccot x, graph of arc-tangent function and arc-cotangent function, arc-cosecant function and arc-secant function, graph of arc-cosecant and arc-secant function, trigonometric equations, basic trigonometric equations, equation sin x = a, equation cos x = a, equation tan x = a, equation cot x = a, equations sin (bx + c) = m, equation cos (bx + c) = m, equation tan (bx + c) = m, equation cot (bx + c) = m where b c and m are real numbers, equations that can be written as f * g = 0, trigonometric equations of quadratic form, equations of type a cos x + b sin x = c,

 Grayson Bell
Grayson BellWellington's Incredible Military and Political Journey: A...
When it comes to military and political...

 Kenzaburō Ōe
Kenzaburō Ōe10 Mind-Blowing Events That Take Place In Space
Welcome to the fascinating world of...

 Joseph Conrad
Joseph ConradThe Astonishing Beauty of Lanes Alexandra Kui: Exploring...
When it comes to capturing the essence of...

 Arthur C. Clarke
Arthur C. ClarkeUnlock the Secrets of Riding with a Twist Of The Wrist
Are you a motorcycle...

 Clay Powell
Clay PowellThe Ultimate Guide to An Epic Adventure: Our Enchanting...
Are you ready for a truly mesmerizing and...

 Ashton Reed
Ashton ReedThe Last Great Revolution: A Transformation That Shaped...
Throughout history, numerous revolutions have...

 Julio Cortázar
Julio CortázarThe Cinder Eyed Cats: Uncovering the Mysteries of Eric...
Have you ever come across a book that takes...

 Theodore Mitchell
Theodore MitchellDiscover the Ultimate Spiritual Solution to Human...
In today's fast-paced, modern...

 Tony Carter
Tony CarterContract Law Made Easy Vol.: A Comprehensive Guide for...
Are you confused about the intricacies of...

 Jackson Blair
Jackson BlairThe Wright Pages Butterbump Lane Kids Adventures: An...
In the magical world of...

 Reginald Cox
Reginald CoxAmerica Nightmare Unfolding In Afghanistan
For more than two decades,...

 Sidney Cox
Sidney CoxCivil Rights Leader Black Americans Of Achievement
When it comes to the civil...
Light bulbAdvertise smarter! Our strategic ad space ensures maximum exposure. Reserve your spot today!
 Duncan CoxFollow ·18.8k
Duncan CoxFollow ·18.8k Aaron BrooksFollow ·3.8k
Aaron BrooksFollow ·3.8k Tyrone PowellFollow ·10.4k
Tyrone PowellFollow ·10.4k Sammy PowellFollow ·4.4k
Sammy PowellFollow ·4.4k Bob CooperFollow ·8.8k
Bob CooperFollow ·8.8k Stephen KingFollow ·13.3k
Stephen KingFollow ·13.3k Ben HayesFollow ·19.4k
Ben HayesFollow ·19.4k Dominic SimmonsFollow ·12.4k
Dominic SimmonsFollow ·12.4k






















